Mitigate elemental sulfur condensation in a compressor knockout drum

Produced natural gas must be compressed for export and further processing on the main processing platform. When sour gas (i.e., gas containing H₂S) is compressed, the compressor discharge gas is used as a seal gas that is routed to the inlet of the first stage of the compressor.

The bleed of sour gas being used as seal gas from higher pressure to lower pressure causes the formation of elemental monoclinic sulfur (S₈) (as a gas) by the condensation of H₂S gas. Monoclinic sulfur (melting point = 119°C and density = 1,980 kg/m³) is stable between 96°C and 119°C. It is insoluble in water but soluble in carbon disulfide (CS₂). Monoclinic sulfur, also called prismatic sulfur, has S₈ ring molecules in the crystalline structure. Monoclinic sulfur transforms to rhombic octahedral crystal sulfur (melting point = 112°C and density = 2,060 kg/m³) below 96°C.

The S₈ is routed to the suction knockout drum (KOD) of the first stage of the compressor, which can cause choking of the suction KOD and, consequently, disruption of the normal compressor operation. This article provides the concept and calculations for S₈ formation and quantification, as well as methods for the mitigation of S₈.

Introduction. In sour gas compression, the purpose is to keep the sour gas in a gaseous state (FIG. 1). The operating pressure and temperature throughout the compression process should be such that it should fall below the monoclinic sulfur sublimation curve and right of the rhombic sulfur sublimation curve. The blue region in FIG. 1 is the expected operating envelope. S₈ does not form, and the sour gas remains in a gaseous state.

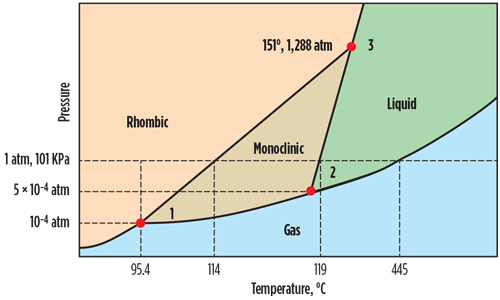FIG. 1. Sulfur phase diagram.

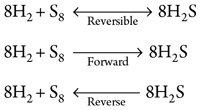
Based on the reaction kinematics and the stoichiometric equation of H₂S formation from its basic elements, H₂ and S₈, the change in free energy of forward formation (Eqs. 1–3) can be calculated:

 

            (1)

 

            (2)

 

            (3)

 From the change in the free energy Arrhenius equation, the equilibrium constant (K_eq) for the forward reaction can be calculated. Once the K_eq value is known, the partial pressure of S₈ at the compressor discharge pressure can be determined.

Knowing the equation for determining the compressor discharge temperature by adiabatic compression, the sulfur phase diagram can be used to determine the operating location and state of sulfur. Similarly, for the reverse reaction, K_eq can be calculated, along with the partial pressure of S₈ at the compressor suction pressure and the bleed outlet temperature. (Note: The change in free energy will be constant; therefore, the free energy change calculated in the forward reaction can be used with the opposite sign in the reverse reaction K_eq calculation.) The outlet temperature may be lower than the compressor suction temperature, and it can be determined by the adiabatic expansion process. Based on the S₈ partial pressure and temperature, the state of the S₈ on the sulfur phase diagram can be checked.

Once the state of the sulfur is known, it can be determined if the sulfur is condensed to liquid and consequently a solid state, and if the temperature is below the melting point. Then, using the partial pressure equation, the mass rate of sulfur condensed into liquid/solid can be calculated.

Calculation basis and assumptions. The calculation basis and assumptions are as follows:

1. Gas expansion though the bleed is an adiabatic process
2. Hydrocarbon fuel gas molecular weight is 35
3. Two-stage compression process is present
4. The change in free energy for the forward reaction is equal to the change in free energy for the reverse reaction with the opposite sign
5. First-stage compressor suction pressure is 100 bar, and temperature is 50°C
6. First-stage discharge pressure is 250 bar, and temperature can be calculated with the adiabatic process gas equation (for this calculation, 65°C is assumed)
7. Second-stage required discharge pressure is 500 bar, and temperature can be calculated with the adiabatic process gas equation (for this calculation, 100°C is assumed)
8. Bleed gas is considered from the second-stage discharge, and flowrate is 1,000 kg/hr
9. Bleed gas outlet pressure is equal to the first-stage suction pressure, which is 100 bar
10. Bleed gas temperature can be calculated with the adiabatic expansion gas equation (for this calculation, 50°C is assumed)
11. Heat capacity ratio of the hydrocarbon gas mixture is 1.4 and is assumed to be constant
12. The compressibility factor of the gas is considered to be 1, for the sake of simplicity
13. H₂S in the compressor suction inlet gas is 50 ppm; therefore, 50 ÷ 10,000 = 0.005 mol% = 0.00005 mole fraction.

Compressor discharge temperature is based on adiabatic compression. If f suction (1) and discharge (2) are known, then Eq. 4 can be used to calculate compressor discharge temperature:

 

 

 

 

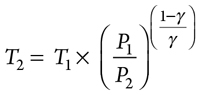            (4)

 

Then, S₈ partial pressure in the forward reaction at compressor discharge pressure and temperature can be calculated, using Eqs. 5–15:

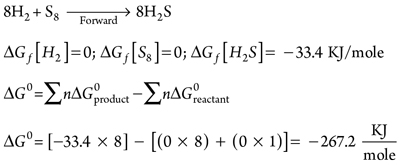        (5)

 

        (6)

 

        (7)

 

        (8)

 

    ∆G⁰ = –267,200 J/mole                                     (9)

    ∆G⁰ = –(R × T)ln(K_eq)                                       (10)

    –267,200 = –(8.314 × (273 + 100)ln(K_eq)          (11)

    86.162 = ln(K_eq)                                               (12)

    K_eq = (2.629) × 10³⁷                                                (13)

 

       (14)

 

 

       (15)

 

 

 

From the forward balance equation stoichiometry, partial pressure of H₂ = partial pressure of S₈⁸, as shown in Eqs. 16–17:

    p_H2 = 8p_s8                                                         (16)

 

 

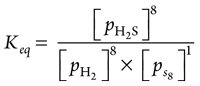              (17)

 

 

Alternatively, see Eqs. 18–21:

 

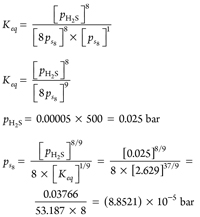              (18)

 

              (19)

 

              (20)

 

 

              (21)

 

 

From these results, it can be ascertained that the state from the sulfur phase diagram at p_s8 = (8.8521) × 10^–5 bar and 100°C is below the S₈ sublimation curve. S₈ partial pressure in the reverse reaction at compressor suction pressure and bleed temperature can be calculated, using Eq. 22–27:

 

               (22)

 

–267,200 = –[8.314 × (273 + 50) ln(K_eq)]               (23)

104.34 = ln(K_eq)                                                    (24)

K_eq = (2.0619) × 10⁴⁵                                            (25)

 

 

          (26)

 

          (27)

 

 

From the forward balance equation stoichiometry, partial pressure of H₂ = partial pressure of S₈⁸, as shown in Eqs. 28–29:

p_H2 = 8p_s8                                                             (28)

 

 

 

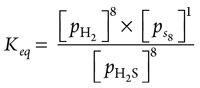               (29)

 

 

Alternatively, see Eqs. 30–33:

 

 

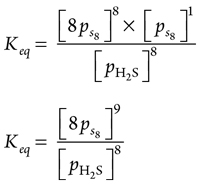               (30)

 

 

 

 

                (31)

 

 

    p_H2 = 0.00005 × 100 = 0.005 bar                        (32)

 

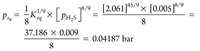               (33)

 

 

From these results, it can be ascertained that the state from the sulfur phase diagram at p_s8 = 0.04187 bar and 50°C is above the rhombic S₈ sublimation curve. It means that H₂S will condense into the compressor suction KOD in the form of rhombic S₈, which will cause compressor damage.

S₈ condensation into liquid/solid in the compressor suction KOD can be quantified, using Eqs. 34–36:

      p_s8 (S₈ partial pressure) = S₈ mole fraction × Total pressure      (34)

      0.04187 bar = S₈ mole fraction × 100 bar              (35)

      S₈ mole fraction = 0.0004187                                (36)

If the total number of moles = 1, then condensed rhombic S₈ moles = 0.0004187. Total assumed bleed gas flowrate = 1,000 kg/hr = 1,000 ÷ 35 = 28.571 kg moles/hr. This means condensed rhombic S₈ = 28.571 × 0.0004187 = 0.01196 kg/hr. In 24 hr, 0.01196 × 24 = 0.2871 kg rhombic S₈ will form in the suction KOD.

Mitigation options. Any proposed mitigation should reduce the equilibrium constant K value. The K value can be reduced by increasing the temperature of the bleed stream and reducing the partial pressure of H₂S in the gas stream. In this experiment, the temperature was increased by electrical heating of the bleed gas pipe. However, the partial pressure of the H₂S could not be reduced below the suction pressure of the first stage.

In conclusion, the results show that bleed stream pressure cannot be reduced below the compressor's first-stage suction pressure. However, the compressor suction hydrocarbon gas stream can be diluted to reduce the mole fraction of H₂S. The second option increases the bleed gas temperature by electrical heating to the temperature of the suction hydrocarbon gas. With these optimizations, the sulfur problem can be solved. GP