Improve gas turbine operation with a reliability analysis
Gas turbines require regular maintenance to ensure reliability and consistent performance. When problems are identified during turbine operation or maintenance inspection, significant engineering work is often required to identify and implement an optimal and effective solution.
In this study, the authors present technical data gathered in the field and from the history of an operating gas turbine power plant. These data were used to better assess turbine reliability according to the Weibull distribution and according to maintainability and operating safety availability, as well as to plan preventive maintenance. This application provided an in-depth understanding of the problems encountered, which helped improve the overall reliability of the turbine.
Study aim and outline. Gas turbines have experienced considerable development in many industrial applications in recent years, particularly in power generation. The evolution and success of gas turbines and compressors have been conditioned by improving their technical performance, as well as by improving the availability and maintainability of these machines to optimize their reliability.
Controlling downtime is of utmost importance for any maintenance manager. With this goal in mind, maintenance departments have adopted methods that consider both the technique and organization of turbomachinery maintenance. Maintenance optimization has been achieved with reliability-based maintenance (RBM) and strategies based on failure analysis (the ABC method), as described in this article.1,2,3
The aim of this study is to determine the exact maintenance intervals needed for a gas turbine. This determination is based on two main criteria—one that takes into account the number of working hours and the other that considers the number of startups. To this end, a TITAN 130 (T130) gas turbine is studied to assess its performance, maintenance and reliability.
The T130 turbine is a single-shaft, self-sustaining system that compresses the atmospheric air in its own compressor, increases the energy power of the air in its combustion chamber and converts this power into useful mechanical energy during the expansion process, which takes place in the turbine section. The resulting mechanical energy is transmitted via a coupling to a receiver, which produces the output power for the industrial process (FIG. 1).
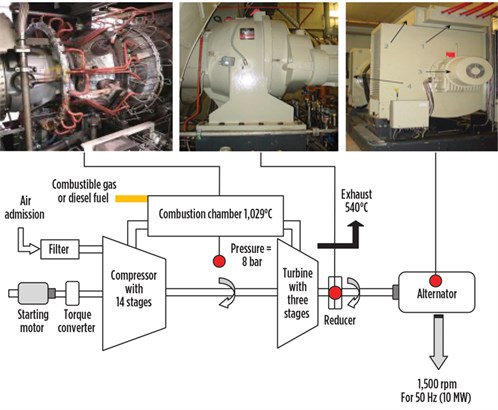 |
| FIG. 1. The working principle of the T130 gas turbine. |
In general, the purpose of maintenance is to guarantee the state of good working order of the production tool, thereby ensuring its availability. Maintenance can also help anticipate system failures. To determine the appropriate maintenance policy, it is first necessary to know the reliability of the equipment.
Statistical study of gas turbine failures. The reliability of a gas turbine is evaluated by obtaining information about its components as they relate to events (failures) occurring during the operation or testing of the equipment.
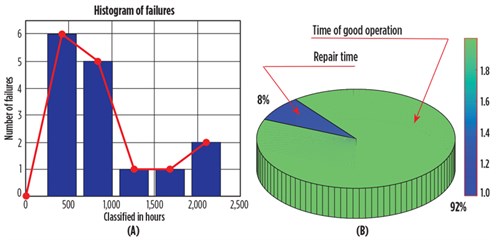
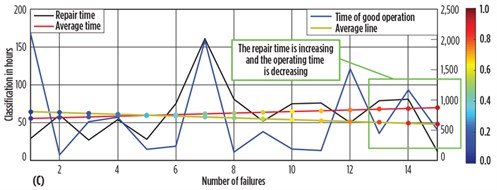
As a first approach to determining reliability, the authors studied the history of functional failures and shutdowns of the turbine over a 2-yr period. This approach consisted of observing a single gas turbine during a certain time of operation and under real conditions of use, and listing all the failures that arose and the information relating to these failures [e.g., time between failure (TBF), time to repair (TTR) and downtime (DT) due to breakdowns]. This list provided the basic data to quantify the reliability of the gas turbine under study. The authors noted that the gas turbine was stopped 15 times in 2 yr for general cleaning, largely as a result of climate exposure. The three graphs in FIG. 2 show other preliminary statistics.
 |
 |
|
FIG. 2. Different failures by classes (A), percentage of uptime vs. repair time in general (B), and statistics study on the history of breakdowns (C). |
In FIG. 2A, it is shown that the greatest number of malfunctions occurred between 0 hr and 420.4 hr. Six recorded malfunctions prove that the turbine is going through a difficult stage in terms of good work. In FIG. 2B, the repair time represents 8% of the time of good operation, which indicates that the repair team is doing well since it has reached a maximum of 17 hr. Finally, in FIG. 2C, a comparison of uptime with repair time shows that the average uptime is decreasing as the repair time increases.
As a preliminary reading of these statistics, the overall system health of this gas turbine is moving closer to the danger zone.
Performance indicators. Performance is a gold mine, not only for production managers, but also for financiers. Performance indicators allow managers to gain a clear picture of the efficiency of a production unit. The performance strategy focuses on the organization of productive resources to improve the availability of the equipment.
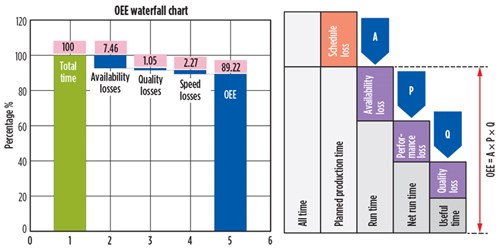
The productivity of equipment is quantitatively monitored by improving the overall equipment effectiveness, or OEE.4,5,6 The OEE is a composite indicator measuring the occupation of a production resource (machine, line or even a production workshop). It is a ratio, calculated as a percentage from 0% to 100%, with 100% representing fully operational equipment and 0% representing equipment with no operational parts.
During the authors’ 2 yr of turbine study, the turbine OEE was found to be low, at between 86.72% and 91.71% (average of 89.22%), mainly due to losses in settings, failures and other shutdowns that negatively influenced equipment performance. The turbine monitoring was based on data collected during this period and used to facilitate the interpretation of OEE tracking results (FIG. 3).
 |
|
FIG. 3. Cascade diagram of the OEE of the studied gas turbine. |
Strategy based on reliability. A reliability analysis strategy (FIG. 4) depends on a balanced relationship between predictive and preventive maintenance. The primary goal of reliability analysis is to analyze the behavior of systems based on their failure rate data. These assessments are also useful for planning activities that help improve operational uptime. The most commonly used method is reliability-centered maintenance (RCM).7,8,9 To implement RCM, the turbine reliability was studied in the context of the Weibull distribution, based on the history of interventions for a limited period of time (14 mos).
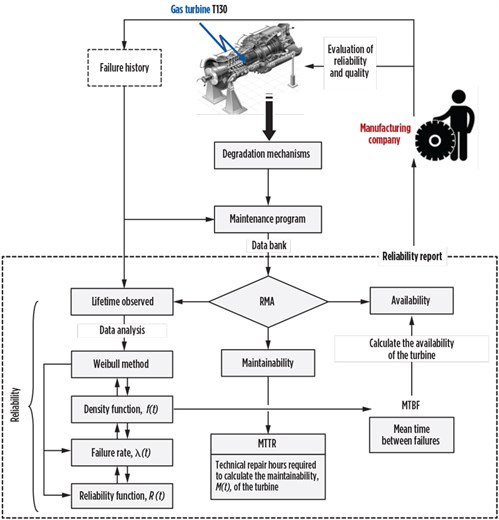 |
| FIG. 4. Method for reliability analysis of the studied gas turbine. |
The reliability of the gas turbine was estimated using the Weibull model, based on the history of interventions shown in TABLE 1. The general form of the reliability function is denoted by R(t), representing the probability of the time between failure at time t (Eq. 1):
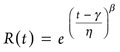 |
(1)
The distribution function, F(t), is the failure probability at t. It is expressed as shown in Eq. 2:
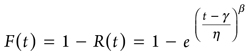 |
(2)
The instantaneous rate of failure, λ(t), is a reliability estimator. It is expressed as shown in Eq. 3:
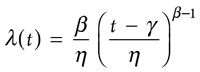 |
(3)
The probability density function, ƒ(t), is calculated using Eq. 4:
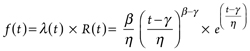 |
(4)
where η is the scale parameter (dimension of t), γ is the location parameter (dimension of t) and β is the shape parameter (dimensionless).
To calculate the aforementioned parameters, the data must be prepared by first determining the pairs (ti, Fi) by the average (median) ranks, as shown in Eq. 5:
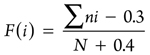 |
(5)
The real history of the T130 gas turbine is used to calculate and plot the reliability indicators, based on the Weibull distribution. TABLE 1 shows the data needed to calculate the Weibull parameters.
Results and discussion. The statistical studies, which used the Weibull model and the value of the variable β > 1, showed that the turbine was heading toward the aging phase. These results could also serve as a diagnosis indicator for maintenance teams to determine the condition of the turbine and predict its future operational state over the short and long terms.
To represent the lifecycle of the studied gas turbine, it is necessary to determine the reliability function, the distribution function, the failure density and the instantaneous failure rate, as illustrated in TABLE 2.
 |
The advantage of the failure density function, f(t), is that it shows the distribution of the failures recorded and the mean time between failures (MTBF). For the turbine studied, the probability density increases when the equipment does not exceed t = 93.59 and decreases when it exceeds this value. Where the distribution function, F(t), is inversely proportional to the reliability, the obtained results (TABLE 2) show that the distribution function rises with the MTBF. This means that the turbine is likely to have significant damages as the time of use increases in the aging phase.
From the perspective of probability, R(t), it is interesting to find the corresponding t in terms of reliability. For a nominal lifetime of L10 associated with the threshold R(L10) = 0.95, for the turbine studied it is equal to 771.6591 hr, which means that the systematic intervening time to maintain a reliability of 95% is t = 771.6591 hr.
Under the given conditions of use, maintainability is the ability of equipment be maintained or restored to a state where it can perform a required function, when maintenance is performed under given conditions, using prescribed procedures and means. The maintainability of a repairable entity is characterized by a probability, M(t), that the maintenance of an entity, E, performed under given conditions (TABLE 3) and with prescribed procedures and means, is completed at time t, knowing that E is at fault time t = 0 (Eq. 6):
 |
M(t) = 1 – eμt (6)
where µ = 1 ÷ mean TTR = 1 ÷ 6 = 0.166666 intervention/hr.
The maintainability is shown to be an increasing curve (FIG. 5), which complements the unity of the probability and ensures that the system is not repaired on the interval (0, t). From the previous results, the system is shown to be maintainable at 63.2% at t = 6 hr.
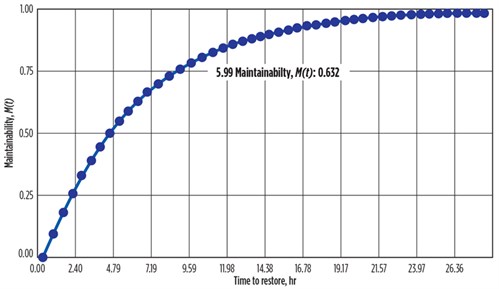 |
| FIG. 5. Estimate of maintainability, using the exponential approximation. |
The availability is shown to be decreasing, and the availability is a reflection of the reliability and maintainability. The change in availability is a direct result of the changes in reliability and maintainability, and the moment of the gas turbine must always act on reliability.
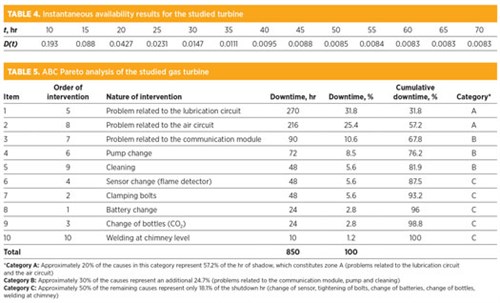
Breakdown analysis of the studied turbine. To apply failure analysis (the ABC method), it is necessary to first make a classification of the failures experienced by the turbine, in descending order of breakdown hours, and then proceed to an ABC Pareto analysis, as shown in TABLE 4.
 |
Takeaway. Gas turbines represent a primary equipment link in the oil and gas production chain, and their reliability is a major concern. In this article, the authors presented a numerical study of the reliability of a T130 gas turbine. The study results showed that improvement in the reliability, maintainability and availability of the gas turbine plays a large role in reducing direct and indirect maintenance costs for equipment and, ultimately, for company operations.
This study also helped establish a database of possible unforeseen failures to be used in predictive and preventive maintenance. Predictive testing and inspection techniques make it possible to increase the service life of the turbine and maintain better reliability. The authors offer the following additional recommendations, based on their turbine reliability study:
- Respect the rules of preventive maintenance
- Apply a standard range of maintenance based on manufacturer recommendations
- Check the reliability of other systems with links to turbine equipment. GP
ACKNOWLEDGMENTS
This work was supported by the Applied Automation and Industrial Diagnostics Laboratory with the Gas Turbine Joint Research Team at the University of Djelfa in Algeria. The authors express their sincere thanks to the staff of the Menia-Ghardaia power station for their kind hospitality during the realization of this work.
LITERATURE CITED
- Zohair, A., A. Hafaifa and S. Abudura, “Operational reliability analysis applied to a gas turbine based on three-parameter Weibull distribution,” Mechanics, Vol. 21, Iss. 3, 2015.
- Saranyasoontorn, K. and L. Manuel, “Efficient models for wind turbine extreme loads using inverse reliability,” Journal of Wind Engineering and Industrial Aerodynamics, Vol. 92, April 2004.
- Meslameni, W., “Optimization of maintenance times of a gas turbine,” International Journal of Applied Research and Technology, Vol. 1, 2018.
- Shen, M. H. H., “Reliability assessment of high cycle fatigue design of gas turbine blades using the probabilistic Goodman diagram,” International Journal of Fatigue, Vol. 21, Iss. 7, August 1999.
- Naikan, V. N. A. and S. Kapur, “Reliability modelling and analysis of automobile engine oil,” Journal of Automobile Engineering, Vol. 220, December 2004.
- Rausand, M., “Reliability centered maintenance,” Journal of Reliability Engineering and System Safety, Vol. 60, 1998.
- Zhang, J., Y. Zhao and M. Xiaobing, “Reliability modeling methods for load-sharing k-out-of-n system subject to discrete external load,” Journal of Reliability Engineering and System Safety, Vol. 193, August 2019.
- Glovatskii, O.-Y., “Operating experience and reliability assessment of elements of pumping stations,” Journal of Hydrotechnical Construction, Vol. 23, Iss. 9, September 1989.
- Zhejun, G., “Estimation of mixed Weibull distribution parameters using the SCEM-UA algorithm: Application and comparison with MLE in automotive reliability analysis,” Journal of Reliability Engineering & System Safety, Vol. 91, Iss. 8, August 2006.
 |
NADJI HADROUG is an Associate Professor with the faculty of science and technology at Djelfa University in Algeria, as well as a member of Djelfa University’s Applied Automation and Industrial Diagnostics Laboratory. He received his PhD from the University of Ziane Achour in Djelfa, Algeria. His work focuses on the development of new methods and tools in fault-tolerant control for industrial systems, and his research interests include the monitoring and control of industrial gas turbine systems. Dr. Hadroug is the author and co-author of several publications and conference papers.
 |
AHMED HAFAIFA is a Full Professor in industrial automation and diagnosis and reliability engineering at the University of Djelfa in Algeria, where he conducts research work in applied automation and industrial diagnostics. He also serves as the Dean of the Science and Technology Department and the Director of the Applied Automation and Industrial Diagnostic Laboratory at the University of Djelfa. Dr. Hafaifa additionally leads the Gas Turbine Joint Research Team in support of several international research projects in the industrial sector. His research interests include control in industrial systems, reliability engineering, fault detection and isolation in industrial processes and intelligent systems based on fuzzy logic and neural networks. He has also published a number of papers in industry journals.
 |
MOSTEFA TELHA is a Professor in the mechanical department of the science and technology faculty at Djelfa University in Algeria. He is preparing his PhD in fluid mechanics at the University of Laghouat in Algeria. He is an engineer in industrial maintenance, and his work focuses on energy systems and the maintenance and diagnostics of mechanical systems.
 |
ABDELHAMID IRATNI is an Associate Professor in control engineering and automation systems in the electrical engineering department of the faculty of science and technology at the University of Bordj Bou Arréridj in Algeria. He has served as the Chair of the scientific committee of the electrical engineering department since 2019, after serving as the head of the bachelor’s and master’s programs since 2015. Dr. Iratni received his BSc and MSc degrees in electrical engineering from the University of Boumerdes in Algeria in 1999 and 2003, respectively. He received his PhD from the University of Sétif in Algeria in 2013. His research areas include nonlinear filtering, estimation and control, biomedical and bioprocess engineering, and automation and reliability of industrial systems.




Comments