Use modeling as part of a compressor maintenance program
D. Halimi and E. Bouali, University of Boumerdès, Boumerdès, Algeria;
A. Hafaifa, University of Djelfa, Djelfa, Algeria; and M. Guemana, University of Médéa, Médéa, Algeria
The automation of industrial systems increases their complexity and cost, consequently reducing their availability. Maintenance is needed to guarantee performance of production equipment. In oil and gas refineries, there is potential for numerous problems related to the reliability of complex processes, such as the turbocompressor bearing system.
A probabilistic modeling approach can be used to determine optimal inspection and repair intervals for the turbocompressor bearing system, as a means of increasing the capacity of transport gas pipelines. This approach has proven reliable in several industrial applications.1–3 It also improves the performance of the turbocompressor and increases the uptime of the bearing system by 28%, or 4,620 operating hours.
The maintenance time line for the turbocompressor depends on the present state of degradation of the bearing system. To maximize maintenance benefits, optimal repair intervals must be determined for the bearing system.4, 5 The compressor (Fig. 1)
examined in this case study is installed in a gas compression plant in Hassi R’Mel, Algeria.
 |
|
Fig. 1. Inspected compression system. |
Industrial plant maintenance. The maintenance of industrial plants represents large annual revenues for several industries.6–9 The gas compression installation in this study is faulty 12% of the time, due to unavailability of the turbocompressor. However, the uptime of the gas compression system can be increased by replacing worn-out equipment, which will also help control the reliability of the bearing system.
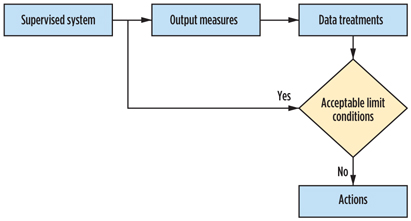
Maintenance effectiveness is a major economic issue in industrial systems. At the examined compressor, conditional preventive maintenance decisions are made as per the flow chart in Fig. 2.
 |
|
Fig. 2. Preventive maintenance. |
Conditional preventive maintenance. This type of maintenance depends on decisions made from plant data (e.g., from diagnosis, sensing and other measurement systems), as shown in Fig. 3. Maintenance decisions should be made by system supervisory teams, as they have a full understanding of each system.6 With informed monitoring, system operations are stopped only when a certain probability of failure exists, as defined by data analyses.
 |
|
Fig. 3. Conditional maintenance structure. |
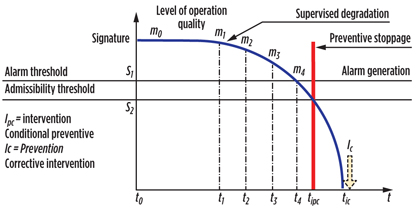
Conditional preventive maintenance is defined as maintenance intervention to be carried out only when the state of the system requires it, as indicated by precise system monitoring.10 Fig. 4 illustrates the principles of conditional preventive maintenance.
 |
|
Fig. 4. Principles of conditional maintenance. |
Conditional maintenance is the preferred solution to increase the performance and improve the level of reliability in a gas compression system.5, 11, 12 It guarantees that the compression system will continue to operate as planned, without breakdown and in a stable manner. This, in turn, stabilizes the quantity of transported gas.
Bearing system. In the oil and gas industry, a variety of equipment is used to guarantee operation under defined conditions.13 This study seeks to determine a reliability model, to be used for the studied gas compression system, which is based on prior studies of bearing systems in centrifugal compressors. This reliability model will be used to increase the productivity of the examined gas compression system.14, 15
Two types of bearing systems are used in centrifugal compressors: elliptical bearings and bearings with swivelling segments. Each end of the tree carries a bearing liner to support the rotor and prevent metal-to-metal contact with the fixed parts in a radial direction. The examined reinjection compressor, which operates under high pressure, uses a bearing system with swivelling segments. The lubricating oil is delivered to the bearing system through small holes, with an effective lubricating oil pressure of approximately 0.7 kg/cm2–0.8 kg/cm2.11
The function of the bearing system in the compressor corresponds to approximately 1%–1.4% of the diameter of the bearing. The dimension of the bearing does not exceed 80 meters per second of the circumferential speed of the tree. The intensity of pressure, which represents the relationship between the weight exerted on the bearing and the available surface, must range between 2 kg/cm2 and 4 kg/cm2, as shown in Eq. 1:16, 17
 (1)
(1)
The radial play and preload of the compressor must also be considered:
 (2)
(2)
In this study, the optimal time line is determined for repairing turbocompressor bearing systems using a probabilistic modeling approach and starting from state parameters that define the state of system degradation. The behavior of the supports corresponds to the actual weight; i.e., each bearing supports a share of the weight of the compressor rotor.
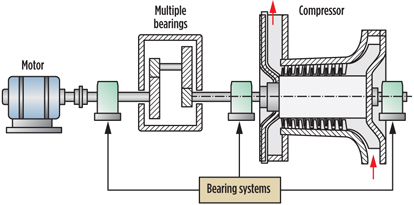
The typical bearing locations in multistage compressors are shown in Fig. 5. There is no excess mass, and, unless the shaft is severely bowed, there should be no misalignment. In high-speed units, couplings, electric motors and gear sets are used, introducing external excitation forces, along with possible unbalancing forces.12
 |
|
Fig. 5. Typical bearing locations in multistage compressors. |
Optimal reliability. In the industrial reliability approach, several optimization methods are utilized.2, 3, 12, 18 For this application, a probabilistic approach was used to determine optimal intervals between inspections for large, complex compressor systems.1 In this approach, reliability is calculated using the probability of the system achieving its intended functions, under specific conditions and in a given length of time. The observation time, T, of the system is a random variable from which the system degradation law can be set.
Eq. 3 presents the probability of the system breaking down during the observation time:
f(t) × dt = P × (t < T ≤ t + dt) (3)
where f(t) is the function of density of probability.
The relation between the distribution of the observation time F(t) and the function of reliability R(t) is given in Eq. 4:
F(t) × dt = P × (T ≤ t) and R(t) × dt = P × (T < t) (4)
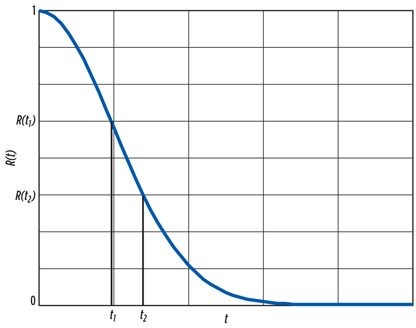
The failure rate, r(t), is the fourth function making it possible to characterize the degradation state of the system. It is the conditional probability of failure per unit of time of a system having survived until time, t. However, the system degradation is completely defined by only one of these characteristics. Reliability is a decreasing function in time, as shown in Fig. 6.
 |
|
Fig. 6. Reliability function. |
In this application, the maintainability measurement can be obtained by statistical testing over the maintenance period. The reliability must be measured against previous studies of bearing system breakdown. The objective here is to find an optimal solution by using a probabilistic approach to satisfy a degree of reliability for repairs, depending on the state of degradation of the compressor bearing system.
Optimization based on probabilistic modeling. The state of degradation of an element is determined by the variations of some state parameter x. If the value of x exceeds a certain threshold, xr, tolerated and defined by the repair technology or operating technical specification, xe, then repair becomes necessary. The variations of parameter x represent a random process in time.1 At the section corresponding to t0 = 0, x has a distribution F(x, t0), with density, f(x, t0), expectation, Ex, 0, and with standard deviation, Sx, 0, as shown in Fig. 7. During the operating time, these characteristics vary, as shown in Eqs. 5 and 6:
Ex, t = Ex, 0 + aE × t (5)
Sx, t = Sx, 0 + aS × t (6)
 |
|
Fig. 7. Diagram of the random process of the x parameter variations. |
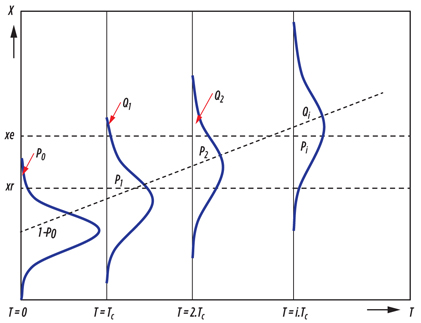
For a given piece of equipment with repair cycle interval, Tc, the total probability of an unplanned intervention after the ith period of the cycle is given in Eq. 7:
 (7)
(7)
where iTc is the time duration until the ith period of the repair cycle, and F(xe, iTc) is the distribution function state parameter, xe, relating to the moment iTc.
The probability of undergoing planned maintenance at time t = iTc is:
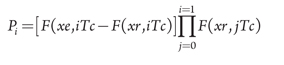 (8)
(8)
By dividing the repair cycle into s intervals, and according to Bayes’ theorem,3 the probability of an unplanned emergency stoppage of equipment is:
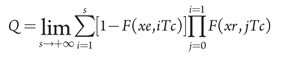 (9)
(9)
The total probability of a component replacement in the equipment under consideration is:
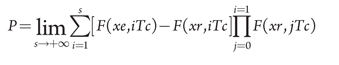 (10)
(10)
In this case, the average service time of the component is:
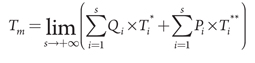 (11)
(11)
where Ti* = (2i – 1) × Tc ÷ 2 and Ti** = i × Tc.
The mathematical expectancy of the possible costs of planned and unplanned maintenance on the equipment, with respect to a given component, is:
E(Tc) = Cd × Q + Cp × P = Cd (Q + λc × P)(12)
where Cd is the total cost of an unplanned intervention and Cp is the total cost of a planned intervention with λc = Cp ÷ Cd.
The specific cost of repair of the element under consideration is:18
Us = E(Tc) ÿ ÷ Tm(13)
where ÿ = (xe – xr) ÷ a × E is the possible average operational duration of the element until failure (x < xr), if preventive maintenance is not performed.
The optimal repair interval is determined by the resolution of Eq. 14:
dUs ÷ dTc = 0(14)
Application results. Under consideration is a turbocompressor with friction surfaces at the journal bearing interface. The surfaces are separated by a continuous layer of lubricant. When the conditions of assembly, operation and lubrication are satisfactory, the lifespan of a journal bearing is primarily dependent on the fatigue strength, and on the actions of the surfaces in contact. Immediately after repair, the contact between the journal and the bearing is not integral, and, after a certain operating time, the texture of the adjusted surfaces becomes blunt, and friction surfaces change. At the same time, the dimensions of the parts vary randomly over time.
The dimensions of worn and new parts can be obtained using a micrometer, and then compared with their nominal values. For journal bearings, wear measurement results obtained at the initial time (t = 0) show that the state variable x follows normal parameters Ex, 0 = 0.18 mm and Sx, o = 0.025 mm. Applying Eqs. 5 and 6 to the results of wear measurement corresponding to 12,000 operating hours of 20 turbocompressors operating under identical conditions gives values of aE = 28.10–8 mm ÷ h and αS = 35.10–8 mm ÷ h. In this case,
xr = 0.3 mm, xe = 0.38 mm and λc = 0.38. The calculation results are presented in Fig. 8.
 |
|
Fig. 8. Dependence of the probabilities Q, P and R on the repair cycle periodicity |
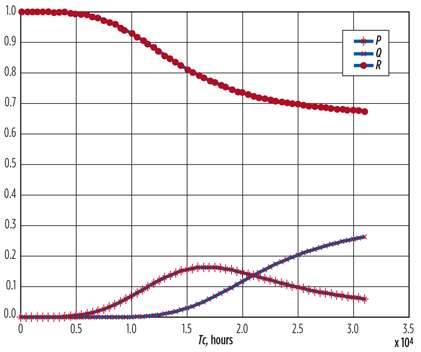
The average time for good performance of the journal bearings up to the repair point was estimated with Eq. 11, and its dependence on period, Tc, is shown in Fig. 9.
 |
|
Fig. 9. Average service time, Tm, of a component. |
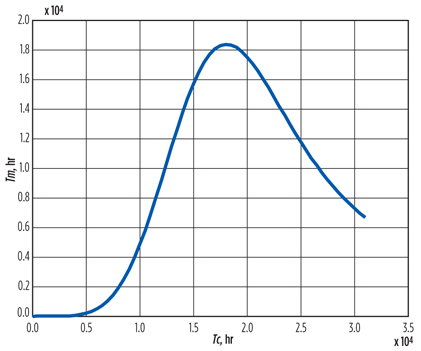
The optimal repair interval of turbocompressor bearings obtained on the basis of Eq. 13 is estimated at 15,500 hours, as shown in Fig. 10.
 |
|
Fig. 10. Specific cost, Us(Tc). |
The comparison of the results obtained, and the value of the repair cycle interval actually implemented, show that a probabilistic approach to maintenance allows for a 28% increase in the working time of the journal bearings. This improvement has great significance, from economical and equipment-availability points of view.
Takeaway. The probabilistic approach discussed here, using an analysis of the repair cycles in a turbocompressor bearing system, shows that it is possible to increase the working time of the bearing system by 28%, or 4,620 operating hours. The probabilistic approach allows for better reliability of the gas compression system and a more accurate estimation of required maintenance intervals. GP
Literature cited
1Yushanov, S. P. and A. E. Bogdanovich, “Analytical probabilistic modeling of initial failure and reliability of laminated composite structures,” International Journal of Solids and Structures, Vol. 35, Nos. 7–8, March 1998, pp. 665–685.
2Zhao, S., B. Zhang and S. Du, “Probabilistic modeling of transient heat transfer and assessment of thermal reliability of fibrous insulation under aerodynamic heating conditions,” International Journal of Thermal Sciences, Vol. 48, No. 7, July 2009, pp. 1,302–1,310.
3Xiang, Y. and Y. Liu, “Application of inverse first-order reliability method for probabilistic fatigue life prediction,” Probabilistic Engineering Mechanics, Vol. 26, No. 2, April 2011, pp. 148–156.
4Nouredine, A., E. Bouali, H. Djamel and M. Guemana, “Recherche des périodicités optimales de réparation des équipements des gazoducs,” Proceeding of the Premier Colloque International, Djerba (Tunisie), Dynamique des Systèmes, des Matériaux et des Structures, IMPACT 2010, March 2010.
5Hafaifa, A., Daoudi and K. Laroussi, “Application of fuzzy diagnosis in fault detection and isolation to the compression system protection,” Control and Intelligent Systems, ACTA Press, July 2011, Vol. 39, No. 3, pp. 151–158.
6Eisinger, S. and U. K. Rakowsky, “Modeling of uncertainties in reliability-centered maintenance—a probabilistic approach,” Reliability Engineering & System Safety, Vol. 71, No. 2, February 2001, pp. 159–164.
7Gregory, L., “Computational intelligence in reliability engineering: Evolutionary techniques in reliability analysis and optimization,” Series: Studies in Computational Intelligence, Vol. 39, 2007.
8Jirutitijaroen, P. and C. Singh, “The effect of transformer maintenance parameters on reliability and cost: A probabilistic model,” Electric Power Systems Research, Vol. 72, No. 3, December 2004, pp. 213–224.
9Hongzhou, W. and P. Hoang, “Reliability and optimal maintenance,” Springer Series in Reliability Engineering, 2006.
10Gaceb, M., B. Rachid and E. Bouali, “Reliability of an unstable conduit used for natural gas transportation,” Safety and Reliability for Managing Risk conference, September 2006, Estoril, Portugal.
11Hendrickson, T. A., J. S. Leonard and D. A. Weise, “Application of magnetic bearing technology for vibration-free rotating machinery,” Naval Engineers Journal, Vol. 99, No. 3, pp. 107–111.
12Chen, H. M. and H. Heshmat, “Principles of Bearing Design,” Compressor Handbook, Paul C. Hanlon, Editor, Chapter 19, McGraw-Hill, New York, New York, 2001.
13Hafaifa, A., F. Laaouad and K. Laroussi, “Fuzzy logic approach applied to the surge detection and isolation in centrifugal compressor,” Automatic Control and Computer Sciences, Vol. 44, No. 1, pp. 53–59.
14Hafaifa, A., F. Laaouad and K. Laroussi, “A numerical structural approach to surge detection and isolation in compression systems using fuzzy logic controller,” International Journal of Control, Automation and Systems, February 2011, Vol. 9, No. 1, pp. 69–79.
15Guemana, M., S. Aissani and A. Hafaifa, “Use a new calibration method for gas pipelines,” Hydrocarbon Processing, August 2011, Vol. 90, No. 8, pp. 63–70.
16Vance, J., F. Zeidan and B. Murphy, “Bearings and their effect on rotordynamics,” Machinery Vibration and Rotordynamics, May 2010, Vol. 1, No. 1, pp. 171–269.
17Tan, K. M. and K. T. Ooi, “Journal bearings design for a novel revolving vane compressor,” International Journal of Refrigeration, January 2011, Vol. 34, No. 1, pp. 94–104.
18Deloux, E., B. Castanier and C. Bérenguer, “Optimisation de la politique de maintenance pour un système à dégradation graduelle stressé,” 7ème Congrès International Pluridisciplinaire Qualité de Sûreté de Fonctionnement, Tangier, Morocco, March 2007.
 |
Djamel Halimi holds a graduate degree in reliability engineering and maintenance from the University of Boumerdès in Boumerdès, Algeria. After working for a short time in the industry, he joined the Laboratory of Reliability of Hydrocarbon Equipment and Materials of the University of Boumerdès. Dr. Halimi earned a magister degree in industrial maintenance tribology in 2003, and a PhD in maintenance based on reliability systems in 2014, both from the University of Boumerdès. He is the author and coauthor of a number of scientific papers and research projects. His research interests include reliability systems, maintenance applications, intelligent and dynamic systems, supervisory control and data acquisition, and diagnostic and reliability optimization.
 |
Elahmoune Bouali holds a graduate degree in hydrocarbon engineering from the University of Boumerdès in Algeria. He received a PhD in safety of integrity engineering systems in 1987 from the University of Oil and Gas in Moscow, Russia. Since 1988, Dr. Bouali has worked as a researcher and director at the University of Boumerdès’ Laboratory of Reliability of Hydrocarbon Equipment and Materials. He has supervised several PhD and master’s degree students, and has published a number of papers in industry journals. His research interests include reliability systems and optimization, maintenance, intelligent systems, oil and gas equipment reliability, pipeline reliability, and vibration detection and isolation.
 |
Ahmed Hafaifa is a senior lecturer in industrial automation and diagnosis and reliability engineering at the University of Djelfa in Algeria, where he conducts research work in applied automation and industrial diagnostics. Mr. Hafaifa is also the director of the Applied Automation and Industrial Diagnostic Laboratory at the University of Djelfa. His research interests include control in industrial systems, reliability engineering, fault detection and isolation in industrial processes and intelligent systems based on fuzzy logic and neural networks. He has supervised several master’s degree students and published a number of papers in industry journals.
 |
Mouloud Guemana holds a graduate degree in engineering from the University of Boumerdès in Algeria. From 1999 to 2003, he completed his post-doctoral research at the University of Boumerdès, where he has worked as an associate professor since 2004. He received a PhD in industrial maintenance in 2012. Dr. Guemana is the author and coauthor of a number of scientific papers and research projects. His research interests include industrial maintenance, reliability systems, dynamic systems, and diagnostic and reliability optimization.




Comments